变频总线控制系统的特点-变频器功率因数是多少?
时间:2016-05-28 11:14 来源:未知 作者:admin 点击:次
变频总线控制系统具有以下特点。
1.对传动进行控制。通过现场总线,沟通上位控制系统和变频器传动之间的联系。通过传递控制字,可以实现对传动的多种控制功能,例如启动,停止,复位,控制斜坡发生器的斜率,以及传递与速度、转矩、位置等有关的给定值或实际值。
以通用变频器为例,其控制如图所示。

图 总线控制示意
2.对传动进行监测。传动内部的转矩、速度、位置、电流等一系列参数或实际值,都可以设定循环发送模式,以满足生产过程中快速的数据传送。
3.对传动进行诊断。准确可靠的诊断信息可以从传动设定的报警、极限和故障字中获得,这样就可以降低传动的停机时间,因而减少了生产的停工时间。
4.对传动参数的处理。生产过程中的所有参数的上传或下载都可以通过读/写参数来完成。
5.方便的扩展。串行通信简化了模块化机械设计的升级问题,使得以后的升级更为简单。
6.减少安装时间和成本。在电缆方面,用双绞线替换了大量传统传动控制电缆,不但降低了成本,而且提高了系统的稳定性。
在设计方面,由于软硬件采用了模块化结构,缩短了现场总线控制安装的工期。
在调试和装配方面,由于采用了模块化的机械配置,可以对系统中功能各自独立的部分进行预先调试。模块化的结构使得系统的安装变得简单快捷。
变频器功率因数是多少? 变频器的输入电流 变频器的输入电流是三相交流电源经全波整流后向滤波电容器C 充电的电路。显然,只有当电源的线电压UL的瞬时值大于电容器两端的直流电压UD 时,才进行充电。所以,输入电流总是出现在电压的振幅值附近,呈不连续的冲击波形式。它具有很大的高次谐波成分。充电电流总是出现在电源峰值附近的有限时间内,呈不连续的脉冲波形。高次谐波的瞬时功率一部分为“ + ”,另一部分为“一”,属于无功功率。这种无功功率使得变频调速系统的功率因数较低,约为 O.7 ~ 0.75 。由于变频器输入侧功率因数较低的原因。不是电流波形滞后于电压,而是高次谐波电流造成的,所以不能通过并联补偿电容器来提高功率因数.而应设法减小高次谐波电流,具体措施就是接入电抗器,接在三相电源与整流桥之间。 直流电抗器,接在整流桥与滤波电容器之间。使用其中一种就有明显效果,两种共同使用可将功率因数提高到 0.95 以上。直流电抗器除了提高功率因数外。还能限制接通电源瞬间的充电涌流。另外,不允许在变频器输出端,即与电动机的连接端并接电容器。
1.变频器输入侧功率因数的特点
(1)畸变因数在变频器的输入电流中,谐波成分很大,所以变频器输入电流的畸变因数v较低,导致功率因数降低。
(2)位移因数高因为变频器输入电流的基波分量基本上是与电源电压同相位的,所以其位移因数很高,几乎等于1。
2.功率因数表的测量结果
(1)功率因数表的特点 功率因数表是根据偶衡表的原理制作的,其偏转角与同频率电压和电流间的相位差有关。所以,它能够准确地测量位移因数。
但对于谐波电流,则由于它在一个周期内所产生的电磁力将互相抵消,对指针的偏转角不起作用,所以功率因数表不能测定畸变因数。
(2)变频器功率因数的测量误区有人用功率因数表来测量变频器输入侧的功率因数,并以此证明使用变频器后,可提高功率因数,这是错误的。因为变频器输入侧的功率因数降低的根本原因,在于其具有相当强的谐波电流,导致畸变因数较低,而功率因数表偏偏不能测定畸变因数。
所以,如果用功率因数表来测量变频器输入侧的功率因数,所得到的结果是错误的。
几个基本定义:
(1)功率因数的定义在交流电路中,把平均功率与视在功率之比,称为
功率因数,即
λ=P/S ( 12-1)
式中λ-功率因数;
P-平均功率,也叫有功功率(kW);
S-视在功率,也叫表观功率(kVA)。
(2)平均功率的定义一个周期内,功率的平均值称为平均功率,即
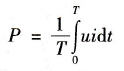 (12-2) (12-2)
式中T-交变电流的周期(s);
u-电压的瞬时值(V);
i-电流的瞬时值(A);
dt-时间的微分(s)。
(3)视在功率的定义电压和电流有效值的乘积,称为视在功率,即
S=UI (12-3)
式中U-电压的有效值(V);
I-电流的有效值(A)。
1.基本分析设:
u=Umsinωt
i=Imsim(ωt-φ)
则
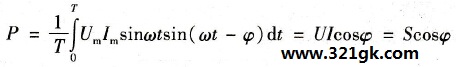 (12-4) (12-4)
式中 Um-电压的振幅值(V);
Im-电流的振幅值(A);
ω-角频率;
t-时间(s);
φ-电流与电压的相位差角。
由式(12-1)和式(12-4),得
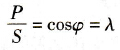 (12-5) (12-5)
式中cosφ-位移因数。
2.结论实际上,λ=cosφ就是同频率正弦电流的功率因数。在电力电子技术未进入实用阶段之前,电气设备中的电流绝大多数都是正弦波。所以,人们通常把电流与电压相位差角的余弦cosφ就定义为功率因数。
1.谐波电流的平均功率对于分析非正弦电流的功率因数来说,了解谐波电流的平均功率是至关重要的。在电工基础里,非正弦电流可以通过傅里叶级数分解成许多谐波电流,或者说非正弦电流可以看成是许多谐波电流的合成。
(1)基本分析今以5次谐波电流为例,分析如下:
设:u=Umsinωt
i5=I5msin5ωt
则:
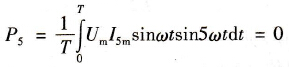 (12-6) (12-6)
式中P5-5次谐波功率的平均值(kW);
i5-5次谐波电流的瞬时值(A);
I5m-5次谐波电流的振幅值(A)。
式(12-6)表明,5次谐波电流的平均功率为0。可以进一步证明,所有各次谐波电流的平均功率都等于0,或者说谐波电流的功率都是无功功率。
(2)物理意义在5次谐波电流的瞬时功率中,一部分是正功率,另一部分是负功率,并且正功率和负功率的总面积正好相等,故平均功率为0,如6.3节中的图6-12所示。
2.非正弦电流的功率因数
(1)基波电流与电压同相位在基波电流与电压同相位的情况下,上述的位移因数可不必考虑。
非正弦电流的有效值由下式计算:
式中I1,I5,I7-基波电流、5次谐波电流和7次谐波电流的有效值(三相对
称电路中不存在以3为倍数的谐波电流)。
因为非正弦电流的无功功率是由于电流波形发生畸变而形成的,故其功率因数用畸变因数来表述,即
式中v-畸变因数。
(2)基波电流与电压不同相 当基波电流的相位与电压相位之间存在相位差时,有:
1)各次谐波电流的平均功率仍为0;
2)基波电流与电压之间因有相位差而产生的位移因数必须考虑。
所以,非正弦电流的功率因数的表达式为
λ=vcosφ (12-9)
(责任编辑:admin) |